算法学习 - 希尔排序

基本思想

  先将整个待排序的序列按照以增量gap=count/2的方式分割成为若干个子序列，再分别进行直接插入排序，待整个序列基本有序，即增量gap=1时，再对全体记录进行依次直接插入排序。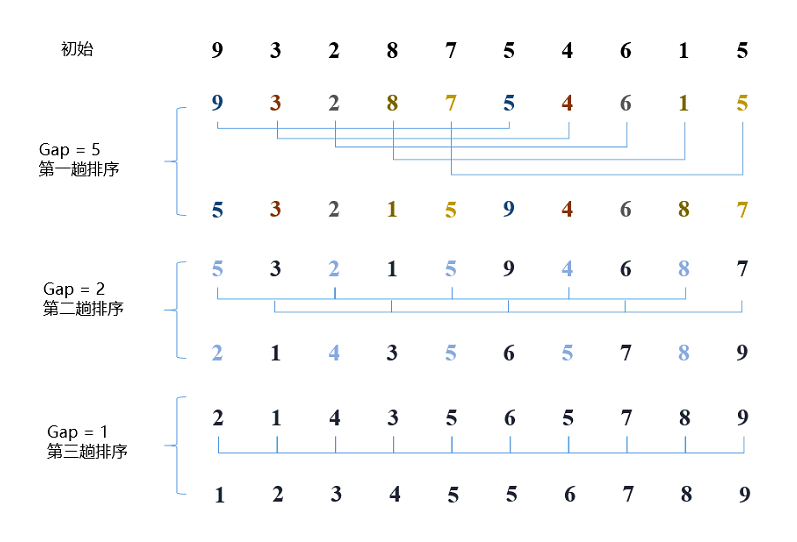


在上图中：
初始时，有一个大小为10的无序序列，颜色相同为一组。
在第一趟排序中，初始增量gap=count/2=5，意味着整个数组被分为5组，[9,5] [3,4] [2,6] [8,1] [7,5]，对这5组数据进行直接插入排序。
在第二趟排序中，我们把上次的增量gap缩小一半，gap=5/2=2，数组被分为2组，[5,2,5,4,8] [3,1,9,6,7]，再对这2组数据进行直接插入排序。
在第三趟排序中，再次将增量缩小为一半，gap=2/2=1，此时，整个数组为1组，[2,1,4,3,5,6,5,7,8,9]，再对最后一组数据进行直接插入排序，排序结束。

Swift 实现

func shellSort(_ array: inout [Int]) {
    var gap = array.count / 2
    var j = 0
    while gap > 0 {
        for i in gap..<array.count {
            let temp = array[i]
            j = i
            while j >= gap && temp < array[j - gap] {
                array[j] = array[j - gap]
                j -= gap
            }
            array[j] = temp
        }
        gap = gap / 2
    }
}

var shellArrays: [Int] = [9, 3, 2, 8, 7, 5, 4, 6, 1, 5]
shellSort(&shellArrays)

稳定性

  由于多次插入排序，我们知道一次插入排序是稳定的，不会改变相同元素的相对位置，但在不同的插入排序过程中，相同的元素可能在各自的插入排序中移动，如上述数据中的5,5，最后其稳定性就会被打乱，所以希尔排序是不稳定的。

时间复杂度

  希尔排序的时间复杂度是根据增量gap有关的。
  在最优的情况下，即元素已经排好序，时间复杂度为：O(n^1.3 )
  在最差的情况下，时间复杂度为O(n^2 )